Graph Y 2 X 2

Nuaja, a subscriber to the IntMath Newsletter, wrote recently:

How do I know how the graph should look similar: For example: y ^two = 10 - two?

The showtime thing I recognize in that equation is the y ^two term, which tells me it volition be a parabola. (It won't be a circle, ellipse or hyperbola because there is an x term, but no 10 ² term. See Conic Sections.)

Allow'due south start with the most bones parabola y = x² and build upward to the required respond.

Example one: y = x ⁱⁱ

You could draw up a table and calculate the y-values for a set of x-values, similar this:

x	-four	-three	-2	-1	0	one	ii	3	iv
y	16	9	4	1	0	i	4	9	sixteen

This gives usa a series of points (-4,sixteen), (-three,9), (-two,4) up to (4,16).

Yous then join these dots with a polish bend and become something similar the post-obit.

Notice that the vertex of the parabola (the "pointy" terminate) is at the origin, (0, 0).

Now for all the curves that I depict below, I'm not going to draw upwardly a tabular array. It becomes slow, and it can lead to incorrect graphs. It is amend to be able to recognize the graph type (from the equation) and and then know how to sketch information technology in the right identify and with the right orientation.

I will consider the effect of pocket-size changes to the equation and then sketch my curve.

All of the following graphs accept the same size and shape as the above bend. I am just moving that curve around to show you how information technology works.

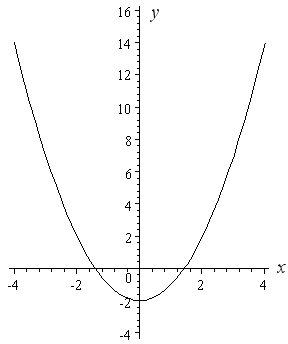
Instance 2: y = x ² − 2

The just difference with the kickoff graph that I drew (y = x ²) and this 1 (y = x ² − two) is the "minus 2". The "minus 2" means that all the y-values for the graph need to be moved down past ii units.

So nosotros merely have our first curve and move information technology downwardly two units. Our new curve'south vertex is at −two on the y-axis.

Next, we run into how to move the bend upward (rather than downward).

Instance 3: y = 10 ² + 3

The "plus 3" means nosotros need to add iii to all the y-values that we got for the basic curve y = x ². The resulting curve is 3 units college than y = x ². Note that the vertex of the curve is at (0, 3) on the y-axis.

Side by side we meet how to movement a bend left and correct.

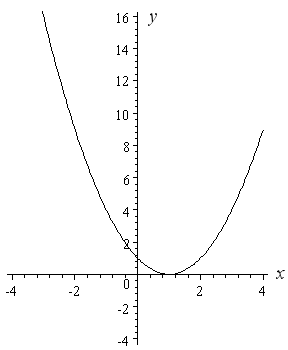
Example 4: y = (x − 1)ⁱⁱ

Note the brackets in this example - they brand a big difference!

If we think near y = (ten − 1)² for a while, nosotros realize the y-value volition always exist positive, except at ten = 1 (where y will equal 0).

Before sketching, I will check another (easy) betoken to make sure I have the bend in the correct place. Putting x = 0 is usually easy, and then I substitute and get

y = (0 − 1)²

= 1

So the curve passes through (0, one).

Here is the graph of y = (x − 1)ⁱⁱ.

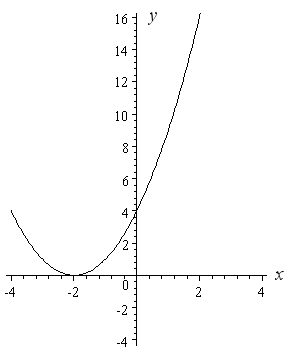
Instance 5: y = (x + two)^two

With similar reasoning to the last instance, I know that my curve is going to exist completely above the x-axis, except at x = −2.

The "plus ii" in brackets has the effect of moving our parabola 2 units to the left.

Rotating the Parabola

The original question from Anuja asked how to draw y² = x − 4.

In this case, we don't have a simple y with an x² term like all of the to a higher place examples. Now nosotros have a situation where the parabola is rotated.

Let's go through the steps, starting with a basic rotated parabola.

Case 6: y ² = x

The curve y ² = x represents a parabola rotated ninety° to the right.

We actually have 2 functions,

y = √x (the elevation half of the parabola); and

y = −√ten (the bottom half of the parabola)

Here is the curve y ^two = ten. It passes through (0, 0) and also (iv,2) and (4,−2).

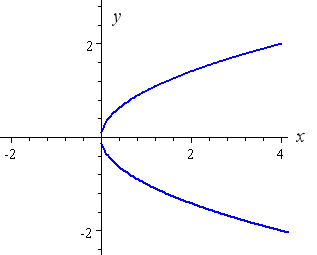
[Observe that we get 2 values of y for each value of ten larger than 0. This is non a function, it is called a relation.]

Example vii: (y + 1)² = x

If we recall about the equation (y + 1)² = 10 for a while, we can see that x volition be positive for all values of y (since any value squared will be positive) except y = −1 (at which bespeak x = 0).

In the equation (y + 1)² = x, the "plus one" in brackets has the issue of moving our rotated parabola downwardly ane unit.

Example 8: (y − 3)^two = x

Using similar reasoning to the in a higher place example, the "minus 3" in brackets has the effect of moving the rotated parabola up 3 units.

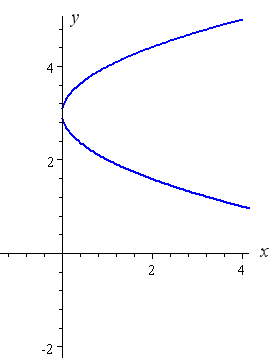
Finally nosotros are set to reply the question posed by Nuaja.

Example 9: y ² = x − 2

Y'all can hopefully imagine what is going to happen now. Nosotros have a y ² term , so it ways it volition be a rotated parabola.

When x = ii, y = 0. The value of x cannot be less than 2, otherwise when we try to evaluate y we would be trying to observe the square root of a negative number. Since out numbers are all real numbers, x must exist greater than or equal to two.

The "minus 2" term has the upshot of shifting our parabola ii units to the right.

I hope you can see at present that if the equation was y ^two = x + 2 (with a "plus"), then we would need to shift our rotated parabola to the left by ii units.

So Nuaja, I hope that answers your question.

Similar all things, the best way how to learn graph sketching is through practice. Too, be observant and note the effect of plus, minus and brackets in each example.

See the 72 Comments beneath.

Graph Y 2 X 2,

Source: https://www.intmath.com/blog/mathematics/how-to-draw-y2-x-2-2301

Posted by: stanfordparrall.blogspot.com

Share this post